Data Clustering Algorithm

군집화 Clustering

데이터를 모아놓았을 때 가장 궁금해하는 것 중 하나. 

 

무슨 데이터가 서로 비슷하고 무슨 데이터가 서로 다른가?

데이터를 서로 유사한 군집으로 나눌 수 없을까?

 

Clustering은 예측이 아닌 분석이다. 즉 정답이 존재하지 않는다. ( Output Variable X)

Unsupervised learning

데이터의 분포나 경향을 파악하기에 좋다.

향후 예측을 위한 사전 단계가 될 수 있다.

 

군집화의 기준은?

데이터간의 유사도

유사한 데이터는 하나의 군집 안에 묶일 수록 좋다.

유사하지 않은 데이터는 서로 다른 군집에 속할 수록 좋다.

유사도는 거리의 역수. → 군집화는 거리 기반.

 

ex)

숫자로된 Data Set을 갖고 있다 가정했을 때

무엇이 이상한 Data?, 무엇이 남과 다른 Data?, 어떤 Data가 서로 비슷한가?

유사함/이상함의 기준은 데이터간의 거리로 생각한다.(distance)

 

군집화를 하는이유

각 군집 별로 패턴을 파악할 수 있다.

각 군집 별로 대응을 분리해서 할 수 있다.

아무 군집에도 속하지 않는 이상한 데이터(특이값)을 찾아낼 수 있다.

 

군집화 방법론

비계층적(non-Hierarchical Clustering) 방법론

• k-means clustering
• DBSCAN

계층적(Hierarchical Clustering) 방법론

• Agglomerative
• Divisive

 

K-means Algorithm

대표적인 분리형 군집화 알고리즘.

중심(centroid)를 가진다. 객

1. 군집의 개수 k를 정한다.

2. k개의 초기 군집중심(centroid)을 설정한다. → 최초에는 random한 값

 

3. 아래 과정을 반복한다.

3.1 모든데이터와 군집 중심 사이의 거리를 계산한다.

3.2 각 데이터를 가장 가까운 군집으로 할당한다. (assign)

3.3 할당된 데이터에 기반해서 군집 중심을 갱신한다 (update)

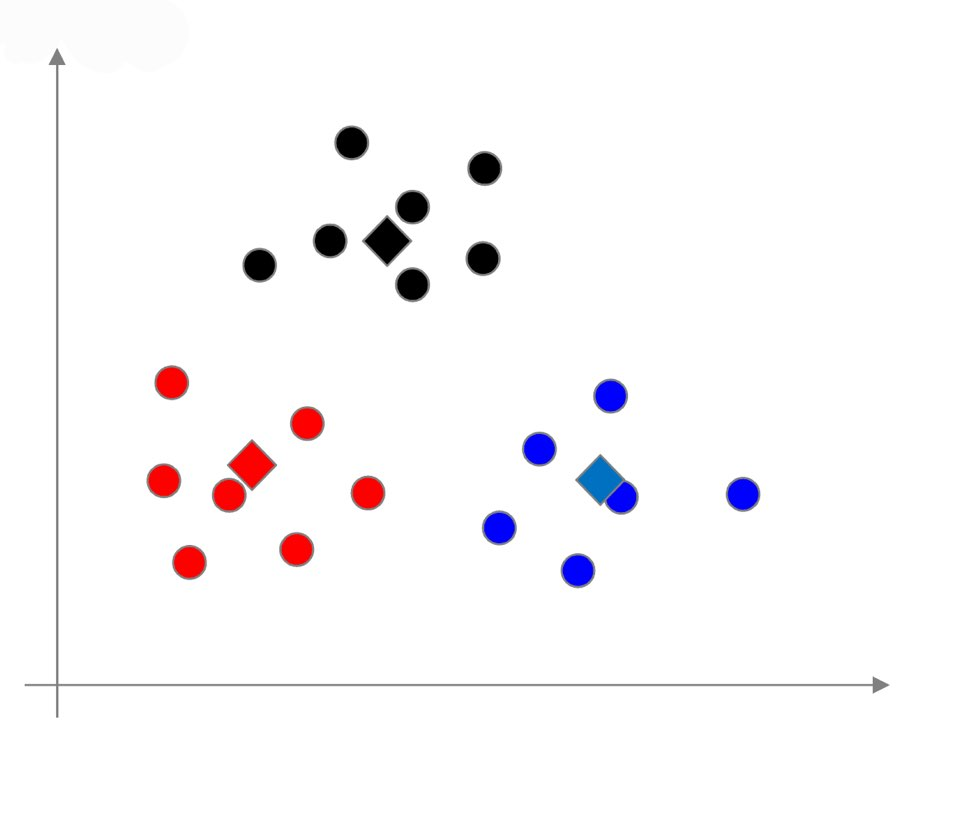
4. 종료조건이 만족하면 알고리즘을 종료한다.

 

K 정하기

 

→ 위에서 정해주는 숫자, 경험적으로 이미 알고 있는 숫자 (과학적이지 못하다)

 

→ 서로 다른 k를 test해보고 좋은 k 정하기

• 서로다른 k에 대해 군집화 결과 평가.
• 가장 좋은 평가를 받은 k를 정한다.
• 정량적 방법(평가를 정량적으로)

좋은 초기 군집중심을 잡으면 좋은 결과를 얻을 수 있다.

단 나쁜 초기 군집중심이 잡히면 회복이 안된다.

 

k-means는 비슷한 크기의 원(구) 형태의 군집을 생성하려는 경향이 있다.

군집 마다 크기, 밀도, 모양이 다를 수 있다.

 

군집화 결과평가

 

Infra/Inter cluster scatter

Infra cluster = 군집 내 거리 = 가까울 수록 좋다. (같은 군집)

Inter cluster = 군집 간 거리 = 멀 수록 좋다. (다른 군집)

 

 

Scatter Ratio

장점

• 직관적으로 이해하기 쉽다.
• 데이터 사이즈에 큰 영향을 받지 않는다. O(nkt)
• 거리계산 + 정렬이므로 구현이 편하다.

단점

• 데이터의 모양 및 밀도에 영향을 받는다
• k값을 정하는 문제와 초기 군집중심을 잡는 문제가 open problem (np 문제)

 

 

 

... 향후 작성 목록 

 

K-medoids Algorithm

 

Centroid-based-clustering Algorithm

 

Single-link Algorithm

 

Completed-link Algorithm

 

 

DBSCAN ( Density-Based Spatial Clustering of Applications with Noise ) Clustering

밀도에 따라 Clustering 하는 알고리즘. 

 

EM (Expectation-Maximization) Clustering

 

Probablistic Latent Semantic Indexing(PLSI)